2022/01/06/THU

lambda

- 예제1: 사용방법

lambda x=1,y=2,z=3 : x+y+z

<function __main__.<lambda>(x=1, y=2, z=3)>

(lambda x=1,y=2,z=3 : x+y+z)()

6

a()

6

a(1,1,1)

3

f = lambda x,y,z : x+y+z 
# lambda 입력:출력 

f(2,3,4)

9

- 예제2: 디폴트입력값

x= (lambda a='fee',b='fie',c='foe': a+b+c) 

x()

'feefiefoe'

x('wee','려치')

'wee려치foe'

예제3: 람다들의 리스트가능

l=[lambda x: x**2, lambda x: x**3, lambda x: x**4] 

iter_l=iter(l)

iter_l.__next__()

<function __main__.<lambda>(x)>

즉 l자체가 iterable object

for a in l: 
    print(a(2))

4
8
16

- 예제4: 람다들의 딕셔너리 가능

dct={'f1': (lambda x: x+1), 'f2': (lambda x: x+22), 'f3': (lambda x: x+333)} 

dct['f1'](1), dct['f2'](1), dct['f3'](1)

(2, 23, 334)

- 예제5: 조건부 출력

(예비학습) 문자열의 대소비교

'a' < 'b' 

True

'c' < 'b'

False

(예제시작)

lower = lambda x,y : x if x<y else y

lower('a','b') 

'a'

lower('c','b') 

'b'

- 예제6 : lambda expression 을 return으로 반환가능

def action(x):
    return (lambda y: x+y)

act = action(99) ## act는 99+y를 수행하는 함수 
act2 = action(98) ## act2는 98+y를 수행하는 함수 

print(act(2)) 
print(act2(2))   # 윗 줄 아랫 줄에 대입된 2는 y자리에 대입된 것이다.

101
100

- 예제7: 예제6의 발전

action = lambda x: lambda y: x+y 
act= action(99)
act2=action(98) 
print(act(2))
print(act2(2))

101
100

map

- 예제1: 사용방법

def inc(x): return x+1

list(map(inc,[1,2,3,4]))

[2, 3, 4, 5]

- 예제1의 변형(람다사용)

list(map(lambda x: x+1,[1,2,3,4]))

[2, 3, 4, 5]

- 예제2: map과 리스트컴프리헨션 비교

f= lambda x: x+2

f(2)

4

이럴 땐 f의 입력으로 int도 가능

f = lambda x: ('1' in x )  

# 내 생각엔 '1' in x 라는 함수 자체에서 x의 입력으로 받을 수 있는 것들이 int형은 안 되는 것 같음

f('a')

False

f('X1'),f('X2'),f('Y1'),f('Y2')

(True, False, True, False)

map

list(map(f,['X1','X2','Y3','Y4']))

[True, False, False, False]

(리스트컴프리헨션과 비교)(중요)

[f(x) for x in ['X1','X2','Y3','Y4']]

[True, False, False, False]

- 예제3: 두개의 입력을 받는 함수(pow) map, 리스트컴프리헨션 비교

(함수소개)

pow(2,4)

16

(map)

list(map(pow,[2,2,2,3,3,3],[0,1,2,0,1,2]))

[1, 2, 4, 1, 3, 9]

(리스트컴프리헨션과 비교)

[pow(x,y) for x,y in zip([2,2,2,3,3,3],[0,1,2,0,1,2])]

[1, 2, 4, 1, 3, 9]

- 예제4: map은 (하나의 함수,다양한 입력)인 경우 사용가능

아래 셀은 함수가 세개라서 사용 불가능

l=[lambda x: x+1, lambda x: x+2, lambda x: x+3 ] 

리스트컴프리헨션은 (다양한함수,다양한입력)이 가능함

[l[i](x) for i,x in zip([0,1,2],[100,200,300])]

[101, 202, 303]

- 종합: 리스트컴프리헨션과 비교하면 (1) 반복인덱스를 쓰지 않는 장점이 있는 반면 (2) 좀 더 제약적으로 사용할 수밖에 없다는 단점이 있음

애드워드 터프티

- 터프티의 이론중 백미: 엄격한 미니멀리즘

• 최소한의 잉크로 많은 정보를 전달할 수 있다면 그것이 바로 좋은 그래프이다.
• 작은 지면 내에서 잉크를 최대한 적게 써서 짧은 시간 안에 많은 영감을 주어야 한다.

- 데이터-잉크비: 데이터를 표현하는데 들아가는 잉크의 양 / 그래픽을 인쇄하는데 들어가는 잉크의 총량

- 차트정크 (나이젤홈즈의 그래프) => 상당히 좋지 않은 차트를 의미함

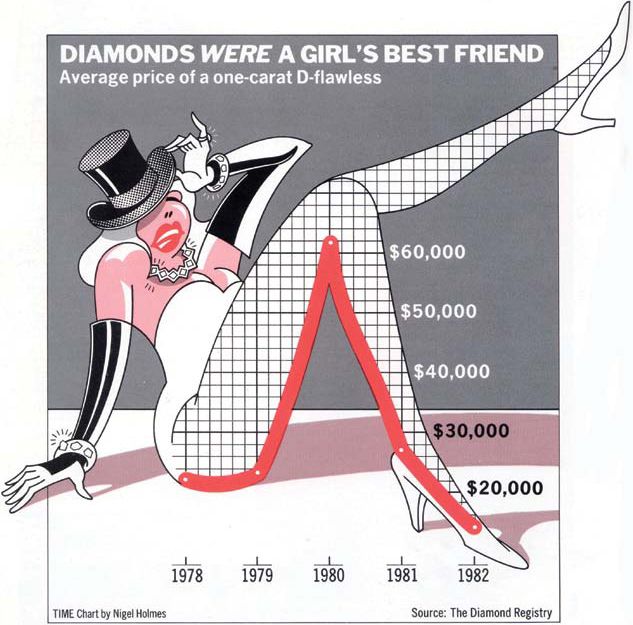
- 별로인 그래프 (왼쪽) / 우수한 그래프 오른쪽

- 별로인 그래프 (왼쪽) / 우수한 그래프 오른쪽

- 별로인 그래프 (왼쪽) / 우수한 그래프 오른쪽

찰스미나드의 도표 (인류역사상 가장 훌륭한 시각화)

• 군대의 크기, 2차원 평면상의 위치, 군대의 이동방향, 모스코바에서 퇴각하는 동안의 여러날짜, 온도 $\to$ 6차원의 변수

- 왜 우수한 그래프일까?

• 자료를 파악하는 기법은 최근까지도 산점도, 막대그래프, 라인플랏에 의존
• 이러한 플랏의 단점은 고차원의 자료를 분석하기 어렵다는 것임
• 미나드는 여러그램을 그리는 방법 대신에 한 그림에서 패널을 늘리는 방법을 선택함.

예제

import pandas as pd
x=[44,48,49,58,62,68,69,70,76,79] ## 몸무게 
y=[159,160,162,165,167,162,165,175,165,172] ## 키
g= 'f','f','f','f','m','f','m','m','m','m'
df=pd.DataFrame({'w':x,'h':y,'g':g})

df

	w	h	g
0	44	159	f
1	48	160	f
2	49	162	f
3	58	165	f
4	62	167	m
5	68	162	f
6	69	165	m
7	70	175	m
8	76	165	m
9	79	172	m

- 미나드의 접근방법

import seaborn as sns
sns.scatterplot(data=df,x='w',y='h',hue='g')

<AxesSubplot:xlabel='w', ylabel='h'>

아래 셀은 지양하자

figs = sns.FacetGrid(df,col='g')
figs.map(sns.scatterplot,'w','h') 

<seaborn.axisgrid.FacetGrid at 0x1ea09b30220>

- 생각보다 데이터가 정리된 형태에 따라서 시각화에 대한 사고방식이 달라진다. 아래와 같은 자료를 받았다고 하자.

df

	w	h	g
0	44	159	f
1	48	160	f
2	49	162	f
3	58	165	f
4	62	167	m
5	68	162	f
6	69	165	m
7	70	175	m
8	76	165	m
9	79	172	m

df1=df.query("g =='f'")[['w','h']] ## 여성.csv 
df2=df.query("g =='m'")[['w','h']] ## 남성.csv 

df1

	w	h
0	44	159
1	48	160
2	49	162
3	58	165
5	68	162

df2

	w	h
4	62	167
6	69	165
7	70	175
8	76	165
9	79	172

- 데이터프레임을 바꿀 생각을 하는게 쉽지 않다.

(방법1)

df1['g']= 'f' 

df1

	w	h	g
0	44	159	f
1	48	160	f
2	49	162	f
3	58	165	f
5	68	162	f

df2['g']= 'm'

df2

	w	h	g
4	62	167	m
6	69	165	m
7	70	175	m
8	76	165	m
9	79	172	m

pd.concat([df1,df2])

	w	h	g
0	44	159	f
1	48	160	f
2	49	162	f
3	58	165	f
5	68	162	f
4	62	167	m
6	69	165	m
7	70	175	m
8	76	165	m
9	79	172	m

(방법2)

df1=df.query("g =='f'")[['w','h']] ## 여성.csv 
df2=df.query("g =='m'")[['w','h']] ## 남성.csv 

df_=pd.concat([df1,df2],keys=['f','m'])
df_

		w	h
f	0	44	159
	1	48	160
	2	49	162
	3	58	165
	5	68	162
m	4	62	167
	6	69	165
	7	70	175
	8	76	165
	9	79	172

---

df_.index

MultiIndex([('f', 0),
            ('f', 1),
            ('f', 2),
            ('f', 3),
            ('f', 5),
            ('m', 4),
            ('m', 6),
            ('m', 7),
            ('m', 8),
            ('m', 9)],
           )

지금은 index가 튜플형태임

df_.loc[('f',3)]

w     58
h    165
Name: (f, 3), dtype: int64

---

pd.concat([df1,df2],keys=['f','m']).reset_index()

	level_0	level_1	w	h
0	f	0	44	159
1	f	1	48	160
2	f	2	49	162
3	f	3	58	165
4	f	5	68	162
5	m	4	62	167
6	m	6	69	165
7	m	7	70	175
8	m	8	76	165
9	m	9	79	172

pd.concat([df1,df2],keys=['f','m']).reset_index().iloc[:,[0,2,3]]

	level_0	w	h
0	f	44	159
1	f	48	160
2	f	49	162
3	f	58	165
4	f	68	162
5	m	62	167
6	m	69	165
7	m	70	175
8	m	76	165
9	m	79	172

pd.concat([df1,df2],keys=['f','m']).reset_index().iloc[:,[0,2,3]].rename(columns={'level_0':'g'})

	g	w	h
0	f	44	159
1	f	48	160
2	f	49	162
3	f	58	165
4	f	68	162
5	m	62	167
6	m	69	165
7	m	70	175
8	m	76	165
9	m	79	172

(방법3)

df_1=df.query("g=='f'")
df_2=df.query("g=='m'")
pd.concat([df_1,df_2])

	w	h	g
0	44	159	f
1	48	160	f
2	49	162	f
3	58	165	f
5	68	162	f
4	62	167	m
6	69	165	m
7	70	175	m
8	76	165	m
9	79	172	m